Đề kiểm tra học kì II môn Toán Lớp 9 - Năm học 2020-2021 - Đề 4 (Có đáp án)

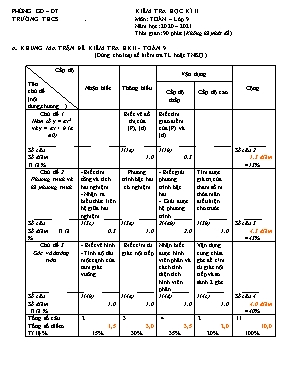
PHÒNG GD – ĐT. 	KIỂM TRA HỌC KÌ II
TRƯỜNG THCS . 	Môn: TOÁN – Lớp 9
	Năm học: 2020 – 2021
	Thời gian: 90 phút (Không kể phát đề)
A. KHUNG MA TRẬN ĐỀ KIỂM TRA HKII - TOÁN 9 
 (Dùng cho loại đề kiểm tra TL hoặc TNKQ) 
 Cấp độ
Tên 
chủ đề 
(nội dung,chương)
Nhận biết
Thông hiểu
Vận dụng
Cộng
Cấp độ thấp
Cấp độ cao
Chủ đề 1
Hàm số y = ax2 
 và y = ax + b (a0)
Biết vẽ đồ thị của 
(P), (d)
Biết tìm giao điểm của (P) và (d)
Số câu 
Số điểm 
Tỉ lệ %
1(1a)
1,0
1(1b)
0,5
Số câu 2
1,5 điểm
=15% 
Chủ đề 2
Phương trình và hệ phương trình
- Biết tìm tổng và tích hai nghiệm
- Nhận ra biểu thức liên hệ giữa hai nghiệm
Phương trình bậc hai có nghiệm
- Biết giải phương trình bậc hai.
- Giải được hệ phương trình
Tìm được giá trị của tham số m thỏa mãn điều kiện cho trước
Số câu 
Số điểm Tỉ lệ %
1(3c)
0,5
1(3a)
1,0
2(4ab)
2,0
1(3b)
1,0
Số câu 5
4,5 điểm
=45% 
Chủ đề 3
Góc và đường tròn
- Biết vẽ hình
- Tính độ dài một cạnh của tam giác vuông
Biết c/m tứ giác nội tiếp 
Nhận biết được hình viên phân và cách tính diện tích hình viên phân
Vận dụng cung chứa góc để c/m tứ giác nội tiếp và so sánh 2 góc 
Số câu 
Số điểm 
 Tỉ lệ %
1(4b)
1,0
1(4a)
1,0
1(4d)
1,0
1(4c)
1,0
Số câu 4
4,0 điểm
=40%
Tổng số câu 
Tổng số điểm
Tỉ lệ %
 2
 1,5
15%
 3
 3,0
30%
 4
 3,5
35%
 2
 2,0
20%
 11
10,0
100%
ĐỀ BÀI
Bài 1(1,5đ) 
a) Vẽ đồ thị của các hàm số sau trên cùng một mặt phẳng tọa độ :
; 
b) Tìm tọa độ giao điểm (nếu có) của (d) và (P).
Bài 2(2,0đ)
a) Giải phương trình 
Giải hệ phương trình 
Bài 3 (2,5đ) Cho phương trình: x2 – mx – 4 = 0 (m là tham số) (1)
Chứng minh phương trình (1) luôn có hai nghiệm phân biệt x1, x2 với mọi giá trị của m.
Tìm giá trị của m để phương trình (1) có hai nghiệm x1, x2 thỏa mãn điều kiện: 
Tìm hệ thức liên hệ giữa x1, x2 không phụ thuộc giá trị của m.
Bài 4 (4,0đ)
Từ một điểm M ở bên ngoài đường tròn (O ; 6cm); kẻ hai tiếp tuyến MN; MP với đường tròn (N ; P (O)) và cát tuyến MAB của (O) sao cho AB = 6 cm.
a) Chứng minh: OPMN là tứ giác nội tiếp
b) Tính độ dài đoạn thẳng MN biết MO = 10 cm
c) Gọi H là trung điểm đoạn thẳng AB. So sánh góc với góc 
d) Tính diện tích hình viên phân giới hạn bởi cung nhỏ AB và dây AB của hình tròn tâm O đã cho.
--------Hết--------
C. HƯỚNG DẪN CHẤM:
ĐÁP ÁN
BIỂU ĐIỂM
Bài 1: 
a)Vẽ đồ thị
Tọa độ điểm của đồ thị 
x
-2
-1
0
1
2
4
1
0
1
4
Tọa độ điểm của đồ thị 
x
0
3
0
(1,5điểm)
0,25
0,25
0,5
b)Phương trình hoành độ giao điểm của (P) và (d)
Có dạng a – b + c = 1 – (-2) + (-3) = 0
 từ (P) 
Vậy : Tọa độ giao điểm của (P) và (d) là 
0,25
0,25
Bài 2: 
a) 
D = (-5)2 – 4.3 = 25 – 12 = 13 > 0 
Vì D > 0 nên phương trình có 2 nghiệm phân biệt
(2,0điểm)
0,5
0,25
0,25
b) 
1,0
Bài 3: Cho phương trình: x2 – mx + m – 1 = 0 (m là tham số) (1)
a) C/m: Phương trình (1) luôn có nghiệm với mọi giá trị của m.
=> Phương trình (1) luôn có nghiệm với mọi giá trị của m
(2,5điểm)
0,25
0,25
0,25
0,25
b) Tìm giá trị của m để phương trình (1) có hai nghiệm x1, x2 thỏa mãn điều kiện: 
+ Theo Viet: x1 + x2 = = m ; x1.x2 = = m – 1 
+ 
 m2 – 2.(m – 1) = 5 
 m2 – 2m + 2 = 5
 m2 – 2m – 3 = 0 
Phương trình có dạng: a – b + c = 1 – (- 2) + (-3) = 0 
Nên: m1 = -1; m2 = 3 
Vậy: m1 = -1 hoặc m2 = 3 thì phương trình (1) có hai nghiệm x1, x2 thỏa mãn điều kiện: 
0,25
0,25
0,25
0,25
c) Tìm hệ thức liên hệ giữa x1, x2 không phụ thuộc giá trị của m.
Ta có: x1 + x2 – 1 = x1.x2 x1 + x2 – x1.x2 = 1 
Vậy: Hệ thức liên hệ giữa x1, x2 không phụ thuộc giá trị của m là: x1 + x2 – x1.x2 = 1
0,25
0,25
Bài 4:
Vẽ hình đúng
(4,0điểm)
0,5
a) Tứ giác PMNO có = 900 và = 900 (Tính chất tiếp tuyến)
 + = 1800 Tứ giác PMNO nội tiếp 
0,5
0,5
b) Tính độ dài đoạn MN: 
Áp dụng định lí Py-Ta –go vào tam giác vuông MON ta có 
 MN = = = 8 cm
0,5
c) Vì: H là trung điểm của AB, nên: OH AB 
= = 900 
 và cùng nhìn đoạn OM một góc 900
 Tứ giác MNHO nội tiếp 
 = ( vì cùng chắn cungMN)
0,25
0,25
0,25
0,25
d) Gọi diện tích cần tính là SVP
	SVP = 
+ Ta có: 0A = OB = AB = 6cm => đều => = 915,59 + = 
	=>SVP = = 6 - 9 = 3(2 - 3) 18,84 - 15,59 3,25 (cm2) 
0,25
0,25
0,25
0,25
* Học sinh có thể giải cách khác, nếu đúng vẫn cho điểm tối đa
--------Hết--------