Bài giảng Toán 9 (Hình học) - Ôn tập chương I. Hệ thức lượng trong tam giác vuông - Trường THCS Thái Sơn

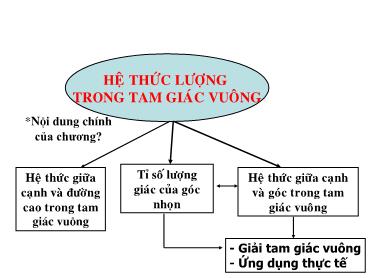
 HEÄ THÖÙC LÖÔÏNG 
 TRONG TAM GIAÙC VUOÂNG
*Néi dung chÝnh 
 của chương?
Heä thöùc giöõa Tæ soá löôïng Heä thöùc giöõa caïnh 
caïnh vaø ñöôøng giaùc cuûa goùc vaø goùc trong tam 
cao trong tam nhoïn giaùc vuoâng
 gi¸c vu«ng
 - Giải tam giác vuông
 - Ứng dụng thực tế 1) Một số hệ thức về cạnh và đường cao trong tam giác 
vuông
 A
 c b
 h
 B c’ H b’ C Câu 1 Cho hình vẽ, ta có hệ thức đúng là: 
 a/ MH2 = NH . NP b/ MH2 = MN2 + MP2
 c/ MN2 = NH . NP d/ MN . MP = NH . HP Câu 2 Trong hình vẽ, ta có DI2 bằng
 a) EI . EF b/ EI . IF
c/ DE . DF d/ DE2 + DF2 Câu 3 Tìm x trong hình vẽ sau:
A . x = 6 C. x = 8
B. x = 7 D . x = 9
x2 = 4.9 x = 36 = 6 Câu 4 Trong hình vẽ, giá trị của x,y bằng
 A
 2
 B x 1
 H C
 A. x = 4 ; y = 2 5 C. x = 2 ; y = 6
 B. x = 2 ; y = 2 2 D. x =1 ; y = 5 Câu 4 Trong hình vẽ, giá trị của x,y bằng
 A
 *.AH2 = HB HC
 2
 2
 x 1 2= x .1
 B H C
 =x 4
 *5BC= HB + HC =
 A. x = 4 ; y = 2 5
 AB2 = HB. BC = 4.5 = 20
 AB =20 = 2 5 2) Tỉ số lượng giác của góc nhọn
 C¹nh huyÒn Câu 1: Chọn kết quả đúng trong các kết quả 
sau:
 Trong hình 1, sin bằng:
 5 5
 A  B 
 3 4
 3 3
 C  D HÌNH 1
 5 4 Câu 2: Chọn kết quả đúng trong các kết quả 
sau:
 Trong hình 2, cos30 0 bằng:
 2a a
 A  B 
 3 3
 3
 C  D 2 3 a2
 2
 HÌNH 2 Câu 3: Chọn kết quả đúng trong các câu sau:
 b a
 A =sin B= tanα
 c c
 b a
 C =cotα D cotα =
 c c
 a c
 b Câu 4: Trong hình 4, hệ thức nào trong các hệ 
thức sau không đúng: 
 A. sin22α + cos α =1
 B. sinα = cosβ
 C. cosβ = sin (900 -α)
 sinα
 D. tanα=
 cosα HÌNH 4 1
Câu 5: Cho sin = thì cos bằng ? 
 2
 2
 A.1 B.
 3
 13
 C. D.
 22
 sin22 + cos = 1
 13
 cos22 = 1 − sin = 1 − =
 44
 3
 cos =
 2 trß ch¬i: gi¶i « ch÷
 Côm tõ gåm 12 ch÷ Cc¸i:ách §iÒu th mµực tÊt hi ệc¶n thÇy c« ®Òu mong ë c¸c em?
 T HMỗi nhIóm §thực hiUện phAép tíHnh cáäc biểuC T è T
 thức. Sau đó, viết các chữ tương ứng 
 1
 2với cá1c kết 3quả tìm3 được3 và2o các 0ô của 2 1 3 1
 3 hàng trên c2ùng 3của bà2i các em sẽ tìm 2 3 3
 được một cụm từ nói về một phong trào 
 mà tất cả các thầy cô đều mong các em 
 0 3 1
 1) sin 60 = thựcA hiện6) tố t = 3
 2 cot600 ô
 2
2) cos450 = C 0 0
 2 7) tan28 .cot28 + 1= 2 H
3) tan300 = 3 U 3
 3 8) cos2120+sin300+sin2120 = §
 2
4) cot450 = 1 I
 1 sin250 1
 0 0 9)  = T
5) tan72 -cot18 = 0 O 3 cos650 3 TIẾT 17 : ÔN TẬP CHƯƠNG I (Tiết 1)
I. LÝ THUYẾT: Bµi 37_SGK/Tr 94)
 Cho tam gi¸c ABC cã 
AB = 6 cm; AC = 4,5 cm; BC = 7,5 cm.
 a) Chøng minh tam gi¸c ABC vu«ng t¹i A. TÝnh 
c¸c gãc B, C vµ ®ưêng cao AH cña tam gi¸c ®ã.
 b) Hái r»ng ®iÓm M mµ diÖn tÝch tam gi¸c MBC 
b»ng diÖn tÝch tam gi¸c ABC n»m trªn ®êng nµo? Bài 37:
b) Hỏi rằng điểm M mà diện tích tam giác MBC bằng diện tích 
tam giác ABC nằm trên đường nào?
H.Dẫn:
 SSMBC= ABC
  A M
 Có cùng chiều cao
 
 M cách BC một khoảng 
 bằng AH B H K C
 
 M nằm trên hai đường thẳng song 
 song với BC và cùng cách BC một M’
 khoảng bằng AH HƯỚNG DẪN VỀ NHÀ
❖ Ôn lại lý thuyết và các bài tập đã giải.
❖ Làm các bài tập còn lại trong SGK.
35,36 SGK/94; 38SGK/95 Bài 38:
 Hai chiếc thuyền 
 ACách và B xác ở vị định trí 
 khoảngđược cách minh giữa họa hai B.
 chiếcnhư thuyền trong đang hình đậu 
 ngoài48. khơi. tính khoảng A.
 cách giữa chúng 
 (làm tròn đến 150
 mét).
 500
 o . .
Dùng tỉ số lượng giác góc 50 tính AI I 380m K t
Dùng tỉ số lượng giác góc 65o tính BI
 Từ đó tính AB