Giáo án Toán học 6 - Chuyên đề 5: Tính đối xứng của hình phẳng trong tự nhiên - Chủ đề 5.2: Hình có tâm đối xứng

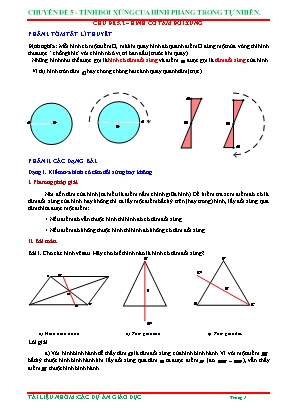
CHỦ ĐỀ 5.2 – HÌNH CÓ TÂM ĐỐI XỨNG
PHẦN I. TÓM TẮT LÍ THUYẾT
Định nghĩa: Mỗi hình có một điểm O, mà khi quay hình đó quanh điểm O đúng một nửa vòng thì hình thu được “chồng khít” với chính nó ở vị trí ban đầu (trước khi quay).
 Những hình như thế được gọi là hình có tâm đối xứng và điểm được gọi là tâm đối xứng của hình.
 Ví dụ hình tròn tâm hay chong chóng hai cánh quay quanh tâm (trục)
PHẦN II. CÁC DẠNG BÀI.
Dạng 1. Kiểm tra hình có tâm đối xứng hay không
I. Phương pháp giải.
	Nói đến t... bình hành dễ thấy tâm là tâm đối xứng của hình bình hành. Vì với một điểm bất kỳ thuộc hình bình hành khi lấy đối xứng qua tâm ta được điểm (đo ), vẫn thấy điểm thuộc hình bình hành.
	b) Với tam giác cân ta phán đoán là tâm đối xứng của hình. Ta chọn điểm thuộc tam giác , khi lấy đối xứng qua ta được điểm (đo ), nhưng điểm không thuộc tam giác . Do đó tam giác cân là hình không có tâm đối xứng.
c) Với tam giác đều ta phán đoán là tâm đối xứng của hình. Ta chọn điểm thuộc tam giác , khi lấy đố...am Á (SEAGAEM)
b) Biểu tượng của Di sản thế giới
(UNESCO)
d) Biểu tượng của Hiệp hội các nước Đông Nam Á (ASEAN)
Bài 3. Trong các hình dưới đây, hình nào có trục đối xứng, hình nào có tâm đối xứng?
Lời giải
	Hình có trục đối xứng là hình b.
Hình d vừa có trục đối xứng, vừa có tâm đối xứng.
Bài 3. Trong các hình dưới đây, em hãy chỉ ra:
	a) Những hình có tâm đối xứng;
Tam giác đều
Cánh quạt
Trái tim
Cánh diều
	b) Những hình có trục đối xứng.
Lời giải
a) Hình có tâm đối xứng là: cá...chắn
f) Giao nhau với
đường ưu tiên
Lời giải
	Biển báo chỉ có trục đối xứng là: e, f, h.
Biển báo vừa có tâm đối xứng, vừa có trục đối xứng: a, b, c, d
Dạng 2. Tâm đối xứng của hình
I.Phương pháp giải.
	Đối với những hình có tâm đối xứng thì hình đó có số cạnh (viền ngoài) là chẵn, hoặc trong thiên nhiên hình ảnh của bông hoa có tâm đối xứng nằm ở giữa (nhị hay nhụy hoa), hình ảnh của cỏ bốn lá cũng có tâm đối xứng.
	Đối với các hình có số cạnh bằng nhau (số cạnh chẵn) thì tâm đối xứng ...ủa hai đường chéo.
e) Hình thang cân không có tâm đối xứng vì với một điểm bất kỳ thuộc hình bình hành khi lấy đối xứng qua tâm ta được điểm , nhưng điểm không thuộc hình thang cân.
Bài 2. Trong mỗi hình dưới đây, điểm có phải là tâm đối xứng không?
a)
b)
c)
d)
Lời giải
Điểm là tâm đối xứng của các hình a, c
a)
b)
c)
d)
Bài 3. Hình nào dưới đây có tâm đối xứng? Em hãy xác định tâm đối xứng (nếu có) của chúng.
Lời giải
Các hình có tâm đối xứng là hình a, b.
Bài 4. Trong các hình d...c chữ cái đó thì chữ cái đó có tâm đối xứng. 
II. Bài toán.
Bài 1. Cho các chữ cái sau, cho biết chữ cái nào có tâm đối xứng và xác định tâm đối xứng của các chữ cái đó.1)
3)
4)
B
2)
5)
6)
E
9)
M
8)
7)
10)
Lời giải
Hình 1: Chữ không có tâm đối xứng.	Hình 2: Chữ có tâm đối xứng chính là điểm .
Hình 3: Chữ không có tâm đối xứng.	Hình 4: Chữ không có tâm đối xứng.
Hình 5: Chữ có tâm đối xứng là điểm .	Hình 6: Chữ không có tâm đối xứng.
Hình 7: Chữ có tâm đối xứng là điểm .	Hình 8...VTV
b)
Bài 3. Trong các hình sau hình nào có trục đối xứng, hình nào có tâm đối xứng?
Lời giải
	Hình a có tâm đối xứng. 	Hình b có trục đối xứng.
Dạng 4. Vẽ hình đối xứng qua 1 điểm.
I. Phương pháp giải.
	Để vẽ điểm đối xứng với điểm A qua ta thực hiện như sau: Dựng đường tròn tâm bán kính OA, đường tròn này cắt lại đường thẳng AO tại điểm khác A. Khi đó điểm là điểm đối xứng với điểm A qua .
Để vẽ được 2 hình đối xứng với nhau qua 1 điểm , ta sẽ chọn một số điểm đặc biệt thuộc hình đó, ... dài bằng . Em hãy vẽ thêm một đường gấp khúc có độ dài bằng để được một hình có cả tâm đối xứng và trục đối xứng.
Lời giải	
Bài 5: Em hãy vẽ thêm vào mỗi hình dưới đây để được các hình có điểm là tâm đối xứng.
Lời giải
Bài 6: Em hãy hoàn thiện hình sau để được một hình nhận điểm O làm tâm đối xứng đồng thời hình đó có trục đối xứng.
Lời giải
Bài 7: Hình gấp khúc dưới đây có độ dài bằng 4 đơn vị. Em hãy vẽ thêm vào hình đó:
a) Một đường gấp khúc có độ dài bằng 6 đơn vị để được một hình có...âm đối xứng là điểm chính giữa của đoạn thẳng hay trung điểm của đoạn thẳng đó. 
Tức là, khi tâm đối xứng của đoạn thì là trung điểm của đoạn thẳng nên: 
Một số hình phẳng có tâm đối xứng thường gặp: hình bình hành, hình vuông, hình chữ nhật, hình thoi, hình lục giác đều:
- Tâm đối xứng của hình bình hành, hình vuông, hình chữ nhật, hình thoi là giao điểm của hai đường chéo. 
- Tâm đối xứng của hình lục giác đều là giao điểm của các đường chéo chính.
Khi đó tâm đối xứng sẽ là trung điểm của...nh khoảng cách từ tâm đối xứng của mặt bàn đến mỗi đỉnh và chu vi của mặt bàn.
Lời giải
	Gọi là tâm đối xứng của mặt bàn.
	Khoảng cách giữa tâm đến mỗi đỉnh của mặt bàn hình lục giác đều là: 	
	Tam giác là tam giác đều nên cạnh của hình lục giác đều là: 
	Chu vi của mặt bàn hình lục giác đều là:
Bài 3: Hình thoi cạnh có tâm đối xứng . Biết . 
a) Tính diện tích hình thoi.
b) So sánh chu vi và diện tích tam giác và tam giác và nhận xét.
Lời giải
	a) là tâm đối xứng của hình thoi nên: là