Đề kiểm tra học kỳ II Toán 8 - Năm học 2022-2023 - Trường THCS Thái Sơn (Có đáp án + Ma trận)

 UBND HUYỆN AN LÃO ĐỀ KIỂM TRA HỌC KỲ II
 TRƯỜNG THCS THÁI SƠN MÔN: TOÁN 8
 Năm học 2022 - 2023
 Thời gian làm bài: 90 phút
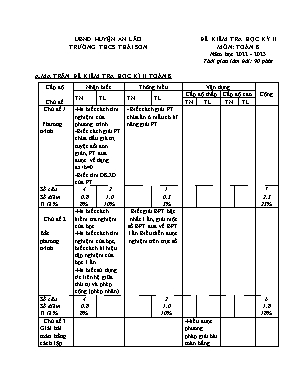
A.MA TRẬN ĐỀ KIỂM TRA HỌC KÌ II TOÁN 8
 Cấp độ Nhận biết Thông hiểu Vận dụng
 Cấp độ thấp Cấp độ cao Cộng
 TN TL TN TL
 Chủ đề TN TL TN TL
 Chủ đề 1 -Hs biết cách tìm - Biết cách giải PT 
 nghiệm của chứa ẩn ở mẫu có kĩ 
 Phương phương trình năng giải PT
 trình -Biết cách giải PT 
 chứa dấu giá trị 
 tuyệt đối đơn 
 giản, PT đưa 
 được về dạng 
 ax+b=0
 -Biết tìm ĐKXĐ 
 của PT
 Số câu 4 2 1 7
 Số điểm 0,8 1,0 0,5 2,3
 Tỉ lệ % 8% 10% 5% 23% 
 -Hs biết cách Biết giải BPT bậc 
 Chủ đề 2 kiểm tra nghiệm nhất 1 ẩn, giải một 
 của bpt số BPT đưa về BPT 
 Bất -Hs biết cách tìm 1 ẩn.Biểu diễn được 
 phương nghiệm của bpt, nghiệm trên trục số
 trình biết cách kí hiệu 
 tập nghiệm của 
 bpt 1 ẩn
 -Hs biết sử dụng 
 t/c liên hệ giữa 
 thứ tự và phép 
 cộng (phép nhân)
 Số câu 4 2 6
 Số điểm 0,8 1,0 1,8
 Tỉ lệ % 8% 10% 18%
 Chủ đề 3 -Hiểu được 
 Giải bài phương 
 toán bằng pháp giải bài 
 cách lập toán bằng phương cách lập PT 
 trình để giải dạng 
 toán chuyển 
 động
 Số câu 1 1
 Số điểm 1,0 1,0
 Tỉ lệ % 10% 10%
 Chủ đề 4 -HS nắm được -HS nắm vững các -HS nắm - Hs vận 
 các t/c của hai trường hợp đồng vững các dụng được 
 Tam giác tam giác đồng dạng của tam giác trường hợp kết quả 
 đồng dạng vuông vận dụng để đồng dạng c/m hai 
 dạng, định -Hs biết cách tính c/m hai tam giác của tam giác tam giác 
 lý Talet. thể tích hình hộp vuông đồng dạng từ vận dụng để đồng dạng 
 Tính chất đã cho, biết cách đó c/m các hệ thức. c/m hai tam để c/m hai 
 đường tính diện tích toàn giác đồng góc bằng 
 phân giác phần hình lăng dạng từ đó nhau từ đó 
 - Hình trụ c/m các hệ c/m được 
 không -Hs biết sử dụng thức quan hệ 
 gian hệ quả đl Talet vuông góc
 tính độ dài đoạn 
 thẳng
 -Hs biết sử dụng 
 t/c đường phân 
 trong tam giác 
 tính tỉ số đoạn 
 thẳng
 Số câu 7 2 1 1 11
 Số điểm 1,4 1,5 1,0 0,5 4,9
 Tỉ lệ % 14% 15% 10% 5% 49%
 Chủ đề 5 -C/m được 
 Cminh bđt
 BĐT
 Số câu 1 1
 Số điểm 0,5 0,5
 Tỉ lệ % 5% 5%
 Tổng câu 17 5 2 2 26
 Tổng điểm 4,0 3,0 2,0 1,0 10
 Tỉ lệ % 40% 30% 20% 10% 100%
B.Đề bài
I. Trắc nghiệm khách quan: (3,0 điểm)
Câu 1: Khẳng định nào “đúng” ?
 A. Hai tam giác vuông luôn đồng dạng với nhau. B. Hai tam giác đều luôn đồng dạng với nhau. 
 C. Hai tam giác đồng dạng thì bằng nhau.
 D. Hai tam giác cân luôn đồng dạng với nhau.
Câu 2: Cho x 2 0 khi đó x nhận giá trị:
 A. x>0 B. x<0 C. x=0 D. x 0
Câu 3: Phương trình x3 = 4x có tập hợp nghiệm là:
 A . 0 ; 2 B . 0 ; 2
 C . 2 ; 2 D . 0 ; 2 ; 2
Câu 4: Cho hình hộp chữ nhật cùng các kích thước đã biết trên hình vẽ (hình 01). Thể tích 
 cm 5
 4 
của hình hộp đã cho là: c
 Hình 1 m
 A . 60 cm2 B . 12 cm3
 C . 60 cm3 D . 70 cm3 
 x x 1
Câu 5: Điều kiện xác định của phương trình 1 là:
 x 3 x
 A. x 3 B. x 0 và x 3 
 C. x 0 D. x 0 và x -3 
Câu 6: Tập nghiệm của phương trình x – 1 = 0 là:
 A. {–1} B. {0} 
 C. {1;0} D. {1} 
Câu 7: Cho bất phương trình: x 2 – 4x 2x – 8. Gía trị nào sau đây là nghiệm của bất 
phương trình ?
 A. x = 3 B. x = 5 
 C. x = 1. D. x = 0 
Câu 8: Cho ABC đồng dạng với HIK theo tỷ số đồng dạng k, HIK đồng dạng với 
 DEF theo tỷ số đồng dạng m. DEFđồng dạng với ABC theo tỷ số đồng dạng
 k
 A. k.m B. 
 m
 m 1
 C. D. 
 k k.m
Câu 9: Trong các phương trình sau, phương trình nào vô nghiệm : 
 A. 8+x = 4 B. 2 – x = x – 4 C. 1 +x = x D. 5+2x = 0
Câu 10 :Tập nghiệm của bất phương trình 5 - 2x 0 là:
 5 5 5 5
 A. {x / x } B. {x / x } C. {x / x } D. { x / x }
 2 2 2 2 Câu 11: Cho hình lăng trụ đứng, đáy là tam giác vuông
cùng các kích thước đã biết trên hình vẽ (hình 02). 
Diện tích toàn phần của hình lăng trụ đã cho là: Hình 02
 A . 288 cm2 B . 960 cm2
 C . 336 cm2 D . Một đáp án khác 
 1
 0
 m c
 c
 m
 8
 m
 12 c
Câu 12: Hình thang ABCD (AB // CD) có các đường chéo cắt nhau tại O. 
 1
Biết OA = AC; AB = 4cm. Độ dài đoạn thẳng CD bằng:
 4
 A. 16 cm. B. 8cm C. 10cm D. 12cm 
Câu 13: Cho ABC , AD là phân giác của góc BAC, D BC. Biết AB=6cm; AC=15cm, 
 BD
khi đó bằng 
 BC
 2 2 5 7
 A. B. C. D. 
 7 5 2 3
 Câu 14: Cho a > b. Khi đó:
 A. a + 2 > b + 2 B. – 3a – 4 > - 3b – 4 C. 3a + 1 < 3b + 1 D. 5a + 3 < 5b + 3 
 2
Câu 15: Cho ABC đồng dạng với HIK theo tỷ số đồng dạng k = , chu vi ABC 
 3
bằng 60cm, chu vi HIK bằng: 
 A. 40cm B. 30cm 
 C. 9 cm D. 9dm 
II. Tự luận(7,0 điểm)
Bài 1(1,5 điểm): Giải các phương trình sau: 
 a) 5x x 3 5x 2 30
 b) 2x 3 5
 x 5 2
 c) 1
 x 1 x 3
Bài 2(1,0 điểm):: Giải bất phương trình và biểu diễn tập nghiệm trên trục số: 
 2
 a) 2x 1 7 x 4x 3 1
 12x 1 9x 3 8x 1
 b) 
 12 3 4
Bài 3 (1,0 điểm): Một ôtô đi từ A đến B với vận tốc 45km/h và quay từ B về A với vận tốc 
40km/h. Tính quãng đường AB biết thời gian đi hÕt ít hơn thời gian về là 1giờ 30 phút. 
Bài 4: (3,0 điểm)
Cho ∆ABC nhọn (AB < AC) có hai đường cao BD và CE cắt nhau tại H. 
 a) Chứng minh: ∆ABD ∽ ∆ACE b) Chứng minh: HD.HB = HE.HC
 IF FA
 c) AH cắt BC tại F. Kẻ FI vuông góc AC tại I. Chứng minh: 
 IC FC
 d) Trên tia đối tia AF lấy điểm N sao cho AN = AF. Gọi M là trung điểm cạnh IC. 
 Chứng minh: NI  FM
Bài 5 (0,5 điểm): 
 1 1 1 1
 Cho a, b, c >0 thỏa mãn abc = 1. CMR: 
 a 2 2b2 3 b2 2c 2 3 c 2 2a 2 3 2 C.HƯỚNG DẪN CHẤM
 I.Trắc nghiệm
Câu 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
Đáp B D D C B D B D C D A D A A D
án
 II.Tự luận:
 Bài Nội dung cần đạt Điểm
 Bài 1 Bài 1: Giải các phương trình sau: 
 (1,5 đ) a) 5x x 3 5x 2 30 (1)
 Giải:
 1 5x 2 15x 5x 2 30 0
 15x 30 0 0,25
 15x 30
 x 2 0,25
 Vậy tập nghiệm của phương trình (1) là: S 2
 b) 2x 3 5(2) 
 Giải:
 0,25
 2x 3 5 2x 8 x 4
 2 
 2x 3 5 2x 2 x 1 0,25
 Vậy tập nghiệm của phương trình (2) là: S 4; 1
 x 5 2
 c) 1(4)
 x 1 x 3
 Giải:
 ĐKXĐ: x 1,x 3 0,25
 x 5 x 3 2 x 1 x 1 x 3 
 4 
 x 1 x 3 x 3 x 1 x 1 x 3 
 x 5 x 3 2 x 1 x 1 x 3 
 0,25
 x 2 3x 5x 15 2x 2 x 2 3x x 3
 x 2 3x 5x 15 2x 2 x 2 3x x 3 0
 2x 10 0
 2x 10
 x 5 (nhận) Vậy tập nghiệm của phương trình (4) là: S 5
Bài 2 Bài 2: Giải bất phương trình và biểu diễn tập nghiệm trên trục số: 
(1 đ) a) 2x 1 2 7 x 4x 3 1(5)
 Giải:
 5 4x 2 4x 1 7 4x 2 3x 1
 4x 2 4x 1 7 4x 2 3x 1 0
 7x 7 0
 7x 7
 x 1 0,25
 Vậy tập nghiệm của bất phương trình (5) là: S x x 1
 Biểu diễn trên trục số: 
 0,25
 )/////////////////////////
 0 1
 12x 1 9x 3 8x 1 
 b) (6)
 12 3 4
 Giải:
 12x 1 4 9x 3 3 8x 1 
 6 
 12 12 12
 12x 1 4 9x 3 3 8x 1 
 12x 1 36x 12 24x 3
 12x 1 36x 12 24x 3 0
 8 0 (vô lý) 0.25
 Vậy tập nghiệm của bất phương trình (6) là: S 
 Biểu diễn trên trục số:
 0,25
 /////////////////////////////////////////////////////////////////
 0
 3
 1 giờ 30 phút = h. Gọi x(km) là quãng đường AB (x>0)
 2 0,25
 Bài 3 x x
 Thời gian đi : (h) . Thời gian về : (h)
 (1.0đ) 45 40
 x x 3 0,25
 Theo đề bài ta có phương trình : 
 40 45 2
 Giải phương trình ta được : x = 540 (thỏa mãn ĐK) 0.25
 Vậy quãng đường AB là 540 km. 0,25 Bài 4: Cho ∆ABC nhọn (AB < AC) có hai đường cao BD và CE cắt 
 nhau tại H. 
 a) Chứng minh: ∆ABD ∽ ∆ACE 
 Giải:
 Bài 4 N
(3,5đ)
 0,2 5
 A
 D
 E
 H I
 M
 K
 B F C
 Xét ∆ABD và ∆ACE có: 
 Aˆ : chung
 0,25
 ˆ ˆ 0
 ADB AEC 90 (vì BD  AC, CE  AB) 0.25
 ∆ABD ∽ ∆ACE (g.g) 
 b) Chứng minh: HD.HB = HE.HC
 Giải:
 Xét ∆HEB và ∆HDC có: 
 ˆ ˆ 0
 HEB HDC 90 (vì BD  AC, CE  AB) 0,25
 EHˆ B DHˆ C (2 góc đối đỉnh) 0,25
 ∆HEB ∽ ∆HDC (g.g)
 HB HE 0.25
 HD.HB HE.HC
 HC HD
 IF FA
 c) AH cắt BC tại F. Kẻ FI vuông góc AC tại I. Chứng minh: 
 IC FC
 Giải:
 Xét ∆ABC có: BD và CE là 2 đường cao cắt nhau tại H 
 H là trực tâm của ∆ABC 0,25
 AH  BC tại F 0.25
 Xét ∆CIF và ∆CFA có: 
 Cˆ : chung 0,25
 FˆIC AFˆC 900 (vì AF  BC, FI  AC)
 0,25
 ∆CIF ∽ ∆CFA (g.g)
 IF FA
 IC FC d) Trên tia đối tia AF lấy điểm N sao cho AN = AF. Gọi M là trung điểm 
 cạnh IC. 
 Chứng minh: NI  FM
 Giải:
 IF FA
 Ta có (do trên) 
 IC FC
 NF
 IF IF NF
 2 (vì AN = AF nên A là trung điểm của NF; 
 2MC FC MC FC
 M là trung điểm của IC)
 Ta có ∆CIF ∽ ∆CFA (do trên)
 Gọi K là giao điểm của NI và MF
 Xét ∆NFI và ∆FCM có: 
 NFˆI FCˆ M (cùng phụ FAˆ C )
 IF NF
 (do trên) 
 MC FC
 ∆NFI ∽ ∆FCM (c.g.c)
 0,25
 FNˆ I CFˆM (2 góc tương ứng)
 Hay FNˆ K CFˆM
 Xét ∆NFK có: FNˆ K NFˆK NKˆ F 1800 (tổng 3 góc trong tam giác)
 CFˆM NFˆK NKˆ F 1800 (vì FNˆ K CFˆM )
 AFˆC NKˆ F 1800
 900 NKˆ F 1800 (vì AF  BC)
 NKˆ F 1800 900
 NKˆ F 900 0,25
 NI  FM 
Bài 6 Ta có: a2 + 2b2 + 3 = (a2 + b2) + (b2 + 1) + 2 
 Áp dụng BĐT x2 + y2 2xy, ta có:
(0.5điểm) a2 + b2 2ab, b2 + 1 2b
 Suy ra: (a2 + b2) + (b2 + 1) + 2 2ab + 2b + 2 = 2(ab + b + 1) 0,25
 a2 + 2b2 + 3 2(ab + b + 1)
 Tương tự: b2 + 2c2 + 3 2(bc + c + 1)
 c2 + 2a2 + 3 2(ca + a + 1) 
 1 1 1 1 
 Do đó: VT (1)
 2 ab b 1 bc c 1 ca a 1 
 Mặt khác: Do abc = 1 nên 1 1 1 1 ab b
ab b 1 bc c 1 ca a 1 ab b 1 b 1 ab 1 ab b
 ab b 1
 1 (2) 0,25
 ab b 1
 1 1 1 1
 Từ (1) và (2) suy ra: 
 a 2 2b2 3 b2 2c 2 3 c 2 2a 2 3 2